Problem Statement

As every engineer knows, each object that exists in memory, eventually has to be broken down into individual building blocks – bits.
For that matter, let’s focus on floating point numbers. As an example, consider a few leading digits of the \( \pi \) number:
$$\pi \approx 3.14159$$
How can we store a value like that in memory?
The most natural thing that might come to your mind would be this:

Let’s store the integer part and the fractional part separately as integers.

This idea would, of course, work but there are a bunch of problems with this attempt that pretty much disqualify
this approach from generic industry-level solutions where performance and space-efficiency is key.

1. We would have to know the length of the fractional part in advance. We might be working with numbers like 3.1 as well as with 0.000012451005 Where do we store the length? Do we fix the value? If so, we would be wasting space for some numbers like 0.5 and might run out of it when we need more precision.
2. Such implementation would certainly cost more memory and as a result require more CPU cycles to load or store the values. Currently, there are two main implementations of floating point numbers – the float (32 bits / 4 bytes) and double (64 bits / 8 bytes). We wouldn’t be able to meet that with our approach.

Recap – how integers are stored in memory

Before we tackle on the more complex problem, let’s make sure we are on the same page and understand the basics. Let’s review the information about integers first. If you find this chapter too trivial, just go ahead and move over to the next one.

Decimal integers

Let’s have a look at some decimal (base 10) and inspect how they are formed.
$$
\begin{align}
42
&= 4 \cdot 10 + 2 \cdot 1 \\
&= 4 \cdot 10^1 + 2 \cdot 10^0
\end{align}
$$

And a bigger one:

$$
\begin{align}
12345
&= 1 \cdot 10,000 + 2 \cdot 1,000 + 3 \cdot 100 + 4 \cdot 10 + 5 \cdot 1 &\\
&= 1 \cdot 10^4 + 2 \cdot 10^3 + 3 \cdot 10^2 + 4 \cdot 10^1 + 5 \cdot 10^0 &\\
\end{align}
$$

Each decimal integer is represented as a sum of the factors of the form $$A \cdot 10 ^ n$$ where \(0 \leq A \leq 9\)

Binary integers

Remember what we reviewed about decimal integers in the previous chapter? The same rule applies to binary integers. With a few tweaks.

1. \(10\) is no longer the base of the system – with binary integers, it’s \(2\)
2. We no longer have \(10\) digits – we only have \(2\) of them

Therefore we can conclude:

Each binary integer is represented as a sum of the factors of the form $$A \cdot 2 ^n$$ where \(0 \leq A \leq 1\)

Examples

$$ \begin{align} \color{red}1\color{green}10\color{blue}1 &= \color{red}{1 \cdot 2^3} + \color{green}{1 \cdot 2^2} + 0 \cdot 2^1 + \color{blue}{1 \cdot 2^0} \\ &= \color{red}8 + \color{green}4 + 0 + \color{blue}1 = 13 \end{align} $$

$$ \begin{align} 10000 &= 1 \cdot 2^4 + 0 \cdot 2^3 + \ldots + 0 \cdot 2^0 = 16 \end{align} $$

Signed and unsigned integers

When writing code, you might come across two technical terms – signed integers and unsigned integers.
Signed integers can store both positive and negative numbers, whereas unsigned integers can only store non-negative numbers.

Integer size

Apart from being signed or unsigned, numeric types are also divided based on their size (the number of bits they take). The most common ones are 8 bits, 32 bits and 64 bits.

Common numeric types

Putting that together, these are the most common integer data types that you can encounter

Data type	Size in bits	Description	Min value	Max value
uint8	8	unsigned integer using 8 bits	0	255
int32	32	signed integer using 32 bits	\(-2^{31}\)	\(2^{31}-1\)
uint32	32	unsigned integer using 32 bits	0	\(2^{31}-1\)
int64	64	signed integer using 64 bits	\(-2^{63}\)	\(2^{63}-1\)
uint64	64	unsigned integer using 64 bits	0	\(2^{64}-1\)

Closer look at the byte

This is the simplest numeric type. In other words, this is an unsigned binary integer composed of eight bits.
In other words, the binary number is eight digits long. Each of these digits can either be \(0\) or \(1\).
The most significant bit (the leftmost one) corresponds to the value of \(2^7 = 128\).
Sample byte:
$$
0\color{red}100\color{green}1\color{blue}10\color{orange}1 = \color{orange}1 + \color{blue}4 + \color{green}8 + \color{red}{64} = 77
$$

Question: What is the lowest number a byte can store?

Of course, we set all of the bits to \(0\) s. The answer is
$$
00000000 = 0
$$

Question: What’s the largest number a byte can store?

Conversely, this time we set all of the bits to \(1\) s. Which yields:

$$
11111111 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255
$$

Question: How do you encode your age into a byte?

Let’s say you are 25 years old. Let’s break that number into a sum of distinct powers of two.

$$
25 = 16 + 8 + 1 = 2^4 + 2^3 + 2^0
$$

So, the bits corresponding to the powers of \(0\), \(3\) and \(4\) need to be set.

$$
00011001
$$

How about uint32?

The datatypes of uint32 and uint64 work in exactly the same way as the byte. The only difference is the number of bits that go into the number.
They use 32 and 64 bits respectively.

For example, that’s a number encoded using the uint32 data type.

$$
100000001 \: 00000001 \: 00000000 \: 00000001
$$

What’s the value of that number?

Question: What’s the largest number you can encode using a uint32?

Set all of the bits to \(1\). As a result, we are getting the following sum:

$$
2^0 + 2^1 + 2^2 + \ldots + 2^{30} + 2^{31} = 2^{32} – 1 = 4,294,967,295
$$

What about negative numbers?

So far, we have only covered positive integers. Now, how are values like \(-5\) stored?
To simplify the reasoning, let’s consider the int8 type (signed, 8 bits)

The first idea you might have would be:

Let’s store the sign as the leading bit – for example, let \(0\) denote \(+\) and \(1\) denote \(-\).

So, going back to int8, The value of \(5\) would be stored as
$$
\color{red}{0}0000101
$$

And \(-5\) as

$$
\color{red}{1}0000101
$$

Yet, this leads to a problem.

Going on with our approach, how do we store zero?

That’s simple, you might be thinking. The answer is:

$$
00000000
$$

You are right. But there is one more number that works just fine.

$$
100000000
$$

So, we have both \(0\) and \(-0\). That’s an inefficiency – we are wasting one slot. There must be a better way to approach this.

Enter: Two’s Complement

The industry-standard approach is called Two’s complement.
It also alters the meaning of the oldest (leftmost) bit, but does it differently.

Let’s say that our number consists of 8 bits. Then, the leftmost bit corresponds to the value of \(-2^7\).
Let’s take a look at two different numbers, one of them is a signed integer, the other one is unsigned (byte).

Unsigned

$$
\color{red}10000011 = \color{red}{2^7} + 2^1 + 2^0 = 131
$$

Signed

$$
\color{red}10000011 = \color{red}{-2^7} + 2^1 + 2^0 = \color{red}{-128} + 2 + 1 = -125
$$

As you can see, two identical binary representations may denote two completely different numbers, based on the underlying data type.

Of course, the same mechanic applies to other signed integers – int32 and int64. The leftmost bits represents:

• \(-2^{31}\) for int32
• \(-2^{63}\) for int64

Floating point numbers

Having covered integers, we can move over to something more complicated – rational numbers.
In order to understand the rationale behind the algorithm, we need to recap the scientific notation first.

Scientific notation – decimal

To put it easily, scientific notation aims to express any number in the form

$$
m \cdot 10^n
$$

Where \(1 \lt m \lt 10\) and \(n\) is an integer.

For example:

$$
23456.789 = 2.3456789 \cdot 10^4
$$

$$
0.00032 = 3.2 \cdot 10^{-4}
$$

Scientific notation – binary

The same principles of scientific notation apply to the binary system. However, for we have fewer digits, so the scientific notation will be of the form

$$
m \cdot 2^n
$$
Where \(1 \lt m \lt 2\) and \(n\) is an integer.

Note: For the case of simplicity, even though we are dealing with binary numbers, I will be writing the fractional part using decimal system.
For example, the binary encoded number \(1.8125\), would be \(1.1101\), which is hard to read.

For example:

$$
2.5 = 1.25 \cdot 2^1
$$
And

$$
5.75 = 1.4375 \cdot 2^2
$$

Floating points in memory – the algorithm

Having done a quick recap of the scientific notation, we are ready to outline the algorithm behind storing floating point numbers in memory.
To do that, we need to efficiently store three piece of data:

• The sign
• The mantissa
• The exponent

Whenever we are storing a floating point value, we are effectively storing the expression of the form
$$
\color{red}{\pm}1.\color{green}{\text{mantissa}}\cdot 2^{\color{blue}{\text{exponent}}}
$$

Consider the float data type. It uses 32 bits. Every number in memory is stored in the following pattern:

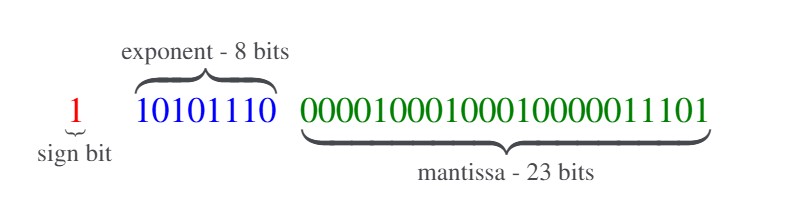
This might be a trifle bit confusing – let’s go through them one by one.

The sign

With floating point numbers, Two’s Complement is not used (like it is with signed integers). The thing is simpler.

• \(1\) denotes negative
• \(0\) denotes positive

The mantissa

This is the most tricky part. Mantissa should be treated as the fractional expansion of the coefficient in scientific notation.
It’s more easily explained with the use of an example.

$$
13.5 = 1.6875 \cdot 2^3
$$

The mantissa is the binary representation of the fractional expansion of the coefficient. In this example, it will be the binary representation of \(0.6875\).
Notice that
$$
0.6875 = \frac 1 2 + \frac 1 8 + \frac{1}{16} = 2^{-1} + 2^{-3} + 2^{-4}
$$
And so the binary representation will be
$$
0.\color{green}{1011}
$$
With \(1011\) being the mantissa.

Now, we also need to remember that the mantissa takes 23 bits – we need to apply padding to the right (Why not to the left? Question to the reader.)
So, the final mantissa is:

$$
\color{green}{10110000000000000000000}
$$

The exponent

The exponent is the unsigned binary representation of the integer to which \(2\) is raised in scientific notation

As you look at the above example, you might be inclined to think the exponent would be \(3\), which is \(11\) in binary.
You would be right. There are just two problems

1. Remember that we have 8 bits for the exponent – we need to apply padding.
2. Since the integer storing the exponent is unsigned, how do we handle negative exponents?

We have 8 bits. This implies that the biggest number we can store on them is \(255\).
The float standard allows us to use exponents from the range \([-126, 127]\)
That means the exponent is biased by 127 (shifted by \(127\))

The exponent is biased. If you want the exponent to be \(3\), you need to encode it as \(3 + 127 = 130\).
If you read a float number whose exponent part is \(120\), you know that the actual exponent is \(120 – 127 = -7\)

So, going back to our example, our exponent will be:

1. Apply bias: \(3 + 127 = 130 = (10000010)_2\)
2. The exponent needs to be \(8\) bits long – but it already is. We don’t need to apply any extra padding – we are done.

Put it all together

We have successfully gathered all components necessary to represent \(13.5 = 1.6875 \cdot 2^3\) as a float.
Let’s put all together.

• sign: \(\color{red}0\)
• mantissa: \(\color{green}{10110000000000000000000}\)
• exponent: \(\color{blue}{10000010}\)

And so the final binary number is:

$$
\color{red}{0} \: \color{blue}{10000010} \: \color{green}{10110000000000000000000}
$$

Uff. That’s been a long way.

Double Trouble

We have covered the float data type which is the most popular one in modern programs.
However, the precision offered by it is often not enough. For such cases, another data type is used –
IEEE 754 double-precision binary floating-point format.
Luckily, it works in exactly the same way as plain old float. The only difference is the size of its components.

• The sign is still \(1\) bit, of course
• The exponent is now \(11\) bits long
• The mantissa is huge – it has \(52\) bits.

Notice how much more precise the double data type is.

Summary

Hopefully, after reading this article you have a pretty good understanding of how integers and floating point numbers
are stored in memory. That is, of course, just the tip of an iceberg. There are more topics to be covered:

• Subnormal numbers
• NaN values
• Precision limitations

If I were to tackle all of them here, the article would transition into a book.
I will elaborate more on those topics in future posts.