The Magic of Approximation

Imagine you’re running a social media platform with millions of users and want to know how many unique visitors you had this month. However, storing every IP address would require gigabytes of memory – a bit too much for a simple counter, isn’t it?

Well, there is an algorithm that can estimate unique counts using only a fraction of the memory. What’s more – it’s shockingly accurate!

HyperLogLog is a brilliant algorithm used in large scale systems to efficiently handle large datasets.

Why counting is hard

There are many counting algorithms and approaches that work very well for small to medium datasets. However, they fall short when massive data comes in.

1. Keeping a full list of visitors – Requires too much memory
2. Using a hashtable – Still needs a space proportional to the number of objects. Also, rehashing and resizing is computationally expensive.
3. Resampling (counting say 1% of the traffic and extrapolating) – Can introduce significant errors

This introduces the challenge: How do we count unique items in a massive dataset without storing them all?

HyperLogLog: An Educated Guess

Let’s think about a different problem for a minute (it is related, I promise).
Imagine we have a regular coin with Heads and Tails.

We perform an experiment – we toss the coin five times and note the outcome.
Question: How many times on average do we have to perform the experiment to obtain 4 heads in a row and a tail at the end?

Of course, the probability of such outcome is 1/32, so on average we need 32 attempts.

Now, imagine that instead of a series of toin flips we have a binary number, where H denotes 0 and T denotes 1.

Assume that we have a streak of N zeros before having a one. How many attempts. on average, did we have to make at generating this binary number? Same principle applies – we need \( 2^{N+1} \) attempts.

How HyperLogLog Works

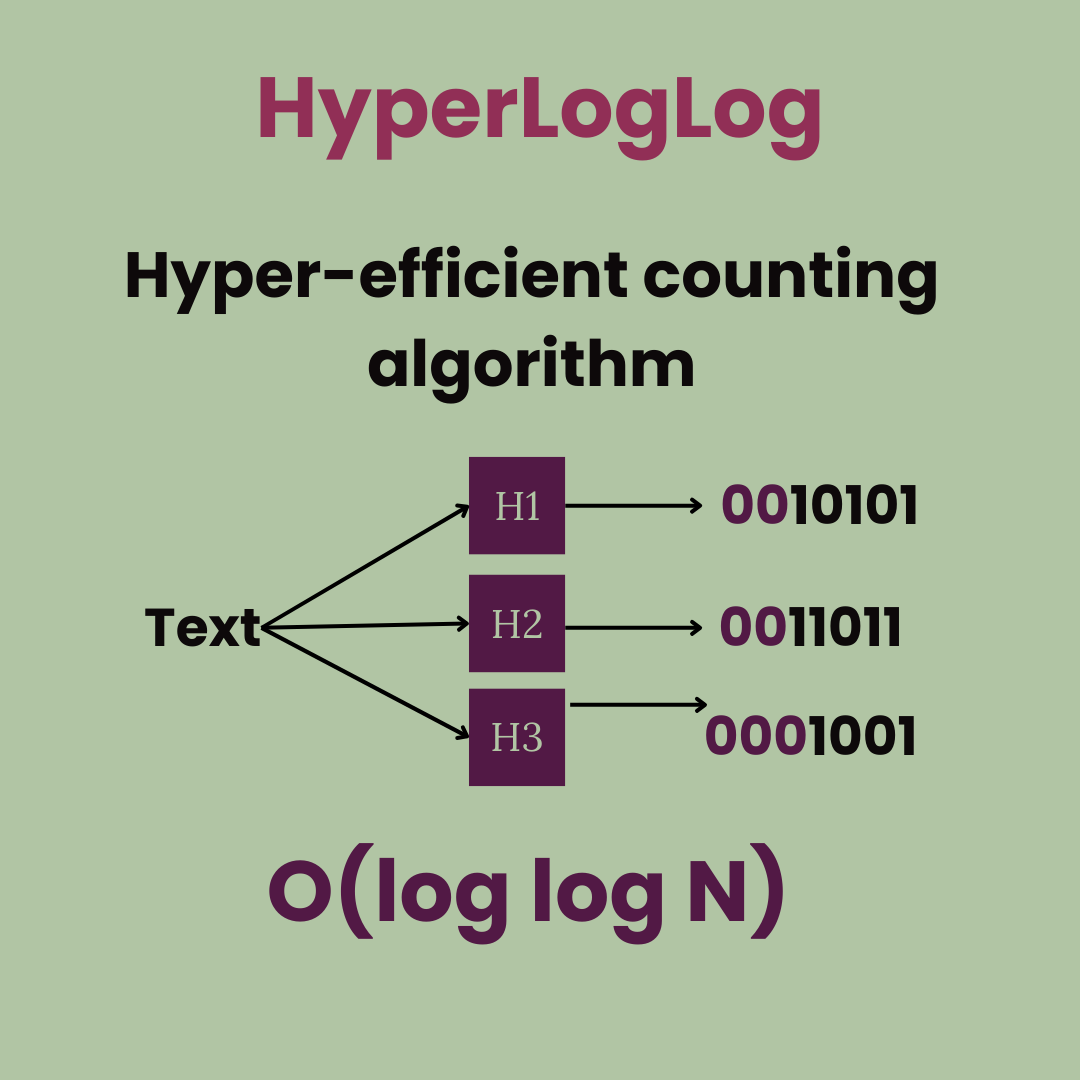
Imagine once again that we have a social media platform where we want to count unique visitors.
We take the IP address of each visitor and then hash it using a hashing function such as md5. Hashing functions have two very important properties

1. The same hash function executed with the same argument will always return the same result
2. Two different numbers will most likely return a different hash (collisions are rare but do occasionally occur)

The resulting hash will have a certain number of zeros before it hits a one

Now, we store only the size of the longest chain of zeros we have seen so far.

Let me explain. The md5 hash has \(128\) bits, meaning there are \(2^{128}\) possible values, which is way more than we’d ever need to count.

Each hash has a certain number of zeros at the beginning (of course it can be zero).

Let’s say that the longest chain of zeros we have seen is 10 characters long. This means, statistically, that we have seen

$$ 2^{11} = 2048 $$ unique IP addresses.

This is our estimation on the number of unique visitors.

Can we improve accuracy?

Absolutely. We can use more hashing functions and track the longest chain of zeros for each one. For example, let’s imagine that we have 5 functions with the following longest chain

Function	Longest chain of zeros
1	12
2	11
3	12
4	11
5	10

Then, the average chain length is

$$ \frac{12+11+12+11+10}{5} = 11.2$$

And so statistically we have seen

$$2^{11.2 + 1} = 2^{12.2} = 4705$$

unique users.

What is the memory usage?

Assume that we have $N$ unique visitors and the maximum length of the chain of zeros is L. It means that

$$ 2^{L+1} = N$$

Which gives us

$$\log_2{N}$$

We only save the number $L$ in memory. In order to save the number in memory, we need

$$\log_2{L}$$ bits.

Which in turn gives us the final complexity

$$\log_2{L} = \log_2 \log_2{N} = O(\log \log N)$$

Conclusion

HyperLogLog is a perfect example of how thinking outside the box can solve impossible problems. Sometimes you don’t need the exact numbers – a smart guess will do!

Feeling a bit overwhelmed with binary number representation? Check out this post where I explain how numbers are stored in memory